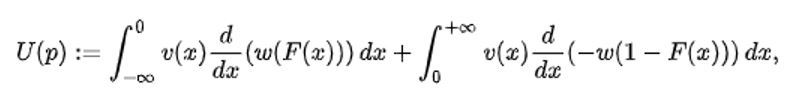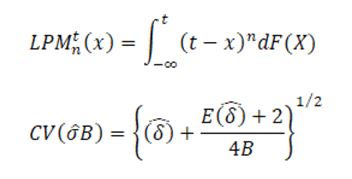Autor: Daniel Alonso Parra
En el campo de la teoría de la inversión financiera estamos asistiendo a cambios sustanciales que afectan tanto al análisis financiero como a la selección de activos para las carteras. Las finanzas tradicionales se sustentaban en una base argumental que defendía que (i) toda causa encontraba un efecto lógico y que (ii) el mercado financiero, por su propia naturaleza, tendía a recuperar la normalidad con el paso del tiempo desde cualquier circunstancia o alteración.
Otra de las máximas tradicionales en el ámbito de la inversión era que la mente humana tenía la capacidad de aprender mecanismos para resolver problemas de forma estructurada y, por tanto, que podía ser entrenada para tomar decisiones de una manera formalmente lógica, sin negar, no obstante, que las emociones influyen negativamente en la toma de decisiones de inversión.
Sin embargo, en un mundo complejo e impredecible como el actual, en el que la información y los datos se suceden torrencial e incesantemente, la teoría tradicional necesita ser complementada con herramientas que permitan depurar la información disponible y convertirla en interpretable para poder optimizar la toma de decisiones y predecir con el menor margen de error posible el comportamiento futuro de los mercados financieros.
El aforismo latino «scientia potentia est», atribuido a Francis Bacon alrededor del año 1597, da a entender que el ‘conocimiento es poder’. Sin duda alguna, casi 500 años más tarde, podríamos definitivamente afirmar que estamos ante una verdad universal y absoluta. El avance de las nuevas tecnologías, en una nueva sociedad capaz de captar la información generada por los individuos, convertirla en datos y procesarlos en un breve lapso de tiempo es la manifestación evidente de que este aforismo tiene la máxima vigencia en todos los ámbitos de nuestra sociedad. Y también la tiene en el sector financiero y, en particular, en la gestión de carteras, donde las decisiones de inversión no pueden tomarse al margen de herramientas estadísticas predictivas que tomen en consideración las diferentes características de los clientes y cuáles son sus objetivos, preferencias y necesidades.
Gestionar inversiones ya no puede basarse sólo en el clásico análisis técnico de valores o centrarse únicamente en los valores fundamentales o en las hipótesis de las teorías tradicionales. Se trata de aceptar que estamos ante una nueva economía de la información en la que los datos son conocimiento y la información es poder. Las “viejas herramientas” se ven superadas por la cantidad de datos y la velocidad con la que se generan, de forma que los gestores de inversiones necesitan herramientas estadísticas que permitan descartar la información no relevante (“ruido estadístico”) y utilizar como relevante aquella que “matemáticamente” ofrezca un porcentaje de correlación con el éxito superior al nivel de riesgo de cada inversor, y todo ello reflejado en números.
Basados en la teoría de la utilidad esperada1 y en la teoría prospectiva2, la estadística y la econometría se han revelado como herramientas esenciales para adaptar el riesgo que el inversor puede asumir y para ayudar al gestor de su cartera a proporcionarle una rentabilidad “interesante” y adecuada a su perfil de riesgo y pretensiones delimitando así un marco teórico bien distinto al que había definido la teoría clásica financiera.
La teoría prospectiva
Esta teoría se basa en un modelo de probabilidades que permite tomar decisiones sobre la base de una función de utilidad que refleja las características de las decisiones tomadas por los seres humanos en materia económica y trata de predecir adecuadamente su comportamiento en momentos de incertidumbre, en los cuales, con frecuencia, los individuos no se comportan de forma racional.
A modo de ejemplo, entre los principales tipos de comportamiento de los individuos ante una inversión podemos obtener los siguientes patrones:
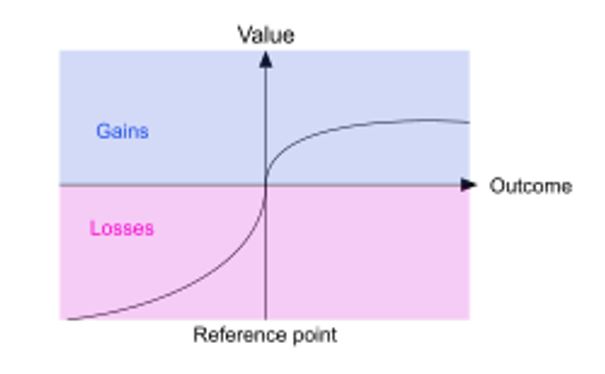
– Los inversores tienen sensibilidad decreciente. A medida que se incrementan las pérdidas o ganancias de una inversión, el impacto de las variaciones de los resultados sobre los inversores disminuye. Esto provoca que éstos sean conservadores en cuanto a las ganancias (prefiriendo una ganancia cierta a otra mayor pero hipotética) y que por el contrario no rechacen arriesgarse a grandes pérdidas si con ello se evita una pérdida menor pero cierta.
La traducción matemática de este comportamiento es que la función de valor es cóncava para el dominio de las ganancias y convexa para el de las pérdidas (gráfico 1).
– Otro comportamiento habitual de los inversores consiste en infravalorar las probabilidades medias y altas de que sucedan ciertos acontecimientos y sobrevalorar las probabilidades de ocurrencia bajas. Así, por ejemplo, las crisis financieras son eventos raros con probabilidades muy bajas que, sin embargo, son sobrevalorados por los inversores.
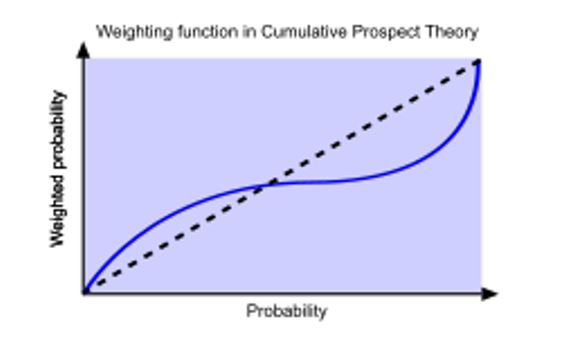
Para reflejar este sesgo, el modelo toma una función de ponderación que transforma de forma no lineal las probabilidades objetivas en probabilidades subjetivas o pesos decisionales (gráfico 2).
En el primer tramo, los pesos decisionales son mayores que las probabilidades objetivas y a medida que crece la probabilidad, los pesos decisionales pierden pendiente y las probabilidades objetivas la aumentan. Así, la función de valor es asimétrica y más pronunciada para las pérdidas que para las ganancias.
En definitiva, la teoría prospectiva analiza el historial de un activo y lo extrapola al futuro. A modo de ejemplo, si un inversor se encuentra por un lado ante un activo financiero que regularmente entrega un 8% de rentabilidad, pero presenta tres drawdown de un 25% anual y, por otro, ante otro activo que con rentabilidades cercanas a un 6% presenta 3 drawdown anuales que no superan el 10%, tiene ante sí cuatro alternativas de inversión: (i) elegir la primera opción, (ii) la segunda, (iii) las dos o (iv) ninguna de ellas. ¿De qué dependerá? Pues simplemente de una cosa; de los objetivos, preferencias y necesidades del inversor y, por tanto, de si la rentabilidad ofrecida por cada opción le parece suficientemente atractiva y le compensa de los posibles sustos (pérdidas momentáneas o parciales) que el activo le ocasionará.
Matemáticamente, la fórmula se expresa de la siguiente forma:
El modelo RReTO
El equipo responsable de la gestión de la cartera de Retto Magnum Inversiones SICAV y en particular su responsable de análisis cuantitativo Maite Alonso Parra junto al autor de este artículo, han desarrollado un modelo aplicado a la gestión bursátil, resultado de años de investigación, que, basándose en el binomio rentabilidad-riesgo, combina los métodos adoptados por los modelos CAPM3-MPT4 y por la teoría prospectiva, al que han denominado RReTo © (Risk Reward Trade Off).
Sus investigaciones y modelos son desarrollos de los ya existentes, si bien perfeccionados desde la óptica de las herramientas matemáticas, informáticas y tecnológicas aplicadas. El resultado es un modelo que no sólo permite delimitar el perfil psicológico del inversor, es decir, el riesgo que está dispuesto a asumir y consecuentemente la rentabilidad que desea obtener, sino que también consigue, mediante un análisis del mercado en el que se incluye el análisis histórico del comportamiento de aproximadamente 2.500 valores, predecir su evolución con gran objetividad.
El modelo valora una inversión por medio de la función de distribución de su rentabilidad y calcula su valor esperado empleando la función de utilidad propuesta por la teoría prospectiva. Asimismo, incorpora un algoritmo cuyo objetivo es minimizar las fluctuaciones inesperadas del mercado.
Para el desarrollo del modelo, RReTO realiza las 21 regresiones lineales correspondientes a los 21 datos incluidos en el registro diario de cotizaciones de un activo financiero concreto y a continuación acomete una serie de combinaciones lineales sobre los residuos obtenidos, otorgando de esta manera un peso mayor a los datos más asimétricos y representativos (esta operación es conocida por el modelo RReTO como get boost rapped5). Con esta operativa matemática se obtiene una función de probabilidad con más de 300 mil datos significativos sobre los sucesos que hubiesen podido acontecer durante el período analizado. Es decir, con esta combinación lineal de los residuos, RReTO consigue alcanzar una objetividad bastante precisa sobre los datos estadísticos más asimétricos y representativos, utilizando una muestra realmente amplia (Gilli y Schumann, 2010).
El siguiente paso que RReTO propone se denomina get parcial moments: a través de la formulación de momentos parciales se analiza el binomio rentabilidad/riesgo y se obtiene una valoración objetiva del activo financiero analizado. Se utilizan cinco órdenes diferentes (0, 1, 2, 3 y 4), indicando un perfil y un grado de aversión al riesgo diferente para cada inversor siendo 0 la aversión al riesgo más baja.
Los momentos parciales inferiores constituyen un conjunto de fórmulas sobre el riesgo que parecen adecuadas para la evaluación de los activos financieros y la construcción de carteras (Balzer, 2001):
Mediante estos cálculos, el modelo extrae una orientación sobre las posibilidades de obtener resultados positivos en una inversión sobre el activo analizado.
Ventajas del modelo
RReTO es no sólo una herramienta más de análisis bursátil sino también un modelo estadístico en sí mismo por todo lo que conlleva: (i) un gran esfuerzo en tiempo, estudio y horas de programación, (ii) el análisis y contraste de teorías económicas aplicables o desechables, (iii) la aplicación práctica del modelo en la propia cartera y (iv) la obtención de una muestra de resultados medibles, fiables y demostrables.
Todo ha sido posible gracias al desarrollo de herramientas matemáticas y teorías económicas que han permitido obtener resultados con mucha menos incertidumbre. Las nuevas herramientas estadísticas posibilitan la eliminación de la curtosis estadística, produciendo un aplanamiento más que sustancial en la curva de las distribuciones, y, además, permiten la identificación de distribuciones normales para obtener una selección de los activos financieros mucho más eficaz. Y todo ello, por supuesto, con la adaptación de la teoría de la utilidad esperada y la teoría prospectiva a la gestión real de carteras.
En definitiva, RReTO tiene una explicación matemática y gráfica, pero también incluye una concepción intelectual sobre la inversión. Se adapta a la libertad del inversor con dos preguntas muy concretas: (i) cuanto quieres ganar y (ii) cuanto estás dispuesto a perder. Una vez respondidas estas dos preguntas, RReTO establecerá qué activos son aptos para el inversor y cuáles no lo son. Las actualizaciones de RReTO nos informarán periódicamente de algunos activos que han dejado de ser aptos y de otros que aparecen como idóneos para ese inversor.
[1] John von Neumann y Oskar Morgenstern, publicaron en 1944 “Theory of Games and Economic Behavior” (Teoría de juegos y comportamiento económico), considerado la piedra angular de la teoría de la utilidad esperada formulada en 1738 por Daniel Bernoulli.
[2] La teoría prospectiva (Prospect Theory) fue desarrollada en 1979 por los psicólogos Daniel Kahneman y Amos Tversky. Esta teoría permite describir cómo los individuos evalúan y toman sus decisiones en situaciones donde deben decidir entre alternativas que comportan riesgo, como sería el caso de la toma de decisiones financieras.
[3] Capital Asset Pricing Model (capm).
[4] Modern Portfolio Theory (MPT).
[5] Basada en el procedimiento de bootstrap desarrollado por Efron y Tibshirani (1986).
Autor:
Daniel Alonso Parra. Gestor de carteras en Solventis SGIIC. Doctorando en economía financiera en la UCLM con la tesis: «La teoría postmoderna de selección de carteras: propuesta RReTO».